Image processing
The concepts of entropy and mutual information have spread far beyond the subject of statistical mechanics and communication theory. Mutual information has been used with great success in image processing, more precisely to perform so called image registration, i.e. the task of deforming one image such that it matches up as well as possible with a given target image. Such algorithms are of great use in medical imaging, where tissues or anatomical regions in the original image can be automatically classified if the target image has already been delineated by a human expert or another algorithm.
Of course “matching up as well as possible” needs to be appropriately defined. For this purpose the mutual information between the intensity distributions of the images can be used. The two images are said to be aligned if they mutual information between them is maximal. This quantity has a major advantage over simple intensity differences as it can also align images made using different devices or under different conditions. In such pairs of images intensities may differ while still being correlated. Consider for example medical images made with X-ray computed tomography (CT) and magnetic resonance imaging (MRI). Bone has a high intensity on CT, but a low intensity on MRI. Even if the images are perfectly aligned, simply subtracting the high and low intensities will result in a large distance. However, when the images are aligned there is a high (negative) correlation between the high and low intensities of bone pixels, resulting in high mutual information.
I have developed a method to match different images based on a principal component analysis of a database of image deformation fields and using mutual information as a matching criterion (Maes et al., 2006; Wouters et al., 2006). Standard registration algorithms make use of either high-dimensional free-form deformations or simple low-dimensional deformations such as scaling and rotation. Free-form deformations however involve a high number of degrees of freedom (of the order of $10^7$ for a typical $200 x 200 x 200$ 3D scan), while simple scaling and rotation cannot capture important anatomical variability. By using principal component analysis I was able to construct a statistical deformation model that is low-dimensional (dimensions of the order of 100) yet at the same time captures the most significant anatomical variability. This dimensionality reduction allows for efficient computation and storage of new deformation fields. Figure 1 shows an example of brain images matched up with my method.
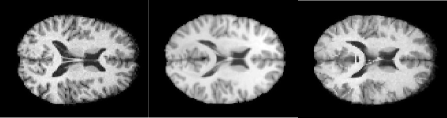
Figure 1: The registration of medical images. Left: a 2D horizontal slice through the original 3D image. Middle: a slice through the deformed image using my statistical deformation method (Wouters et al., 2006). Right: a slice through the target
- Maes, F., D’Agostino, E., Loeckx, D., Wouters, J., Vandermeulen, D., & Suetens, P. (2006). Non-rigid image registration using mutual information. In A. Rizzi & M. Vichi (Eds.), Compstat 2006 - Proceedings in Computational Statistics (pp. 91–103). Physica-Verlag HD.
- Wouters, J., D’Agostino, E., Maes, F., Vandermeulen, D., & Suetens, P. (2006). Non-rigid brain image registration using a statistical deformation model. Proceedings of SPIE, 6144, 614411.