Dimension reduction in multiscale dynamical systems
Many models of physical systems are too complex to be solved analytically, or even numerically if a large range of temporal and spatial scales is involved. For some high-dimensional dynamical systems it is however possible to derive lower-dimensional reduced models (Huisinga et al., 2003; Givon et al., 2004). The reduced model is easier to solve analytically and faster to integrate numerically, while still preserving some of the essential characteristics of the full system. This line of research lies at the heart of many applications, for example in molecular dynamics (Hijón et al., 2009; Lu & Vanden-Eijnden, 2014) and climate modeling (Lucarini et al., 2014; Imkeller & von Storch, 2001; Palmer & Williams, 2009).
The derivation of a reduced model is possible in the presence of a time scale separation between slow resolved and fast unresolved systems, as is done in the homogenisation method (Pavliotis & Stuart, 2008). This method applies to slow-fast systems of the form
\[\begin{align} \dot{x} & = f_0 (x, y) + \frac{1}{\varepsilon} f_1 (x, y) \\ \dot{y} & = \frac{1}{\varepsilon^2} g_1 (x, y) + \frac{1}{\varepsilon} \beta(y) \dot{W}, \end{align}\]where $\dot{W}$ is a standard Brownian motion, in the limit of inifinite time scale separation $\varepsilon \rightarrow 0$. It is evident from the dynamical equation that the $y$ variables evolve on on a faster time scale than the $x$ variables. For finite values of $\varepsilon$ there is an intricate feedback between the evolution of the $x$ and $y$ variables. The situation simplifies, however, in the limit of $\varepsilon \rightarrow 0$ where the slow variables barely evolves on the time scales that $y$ strongly fluctuates. As a result, the slow dynamics converges to a stochastic evolution, where the effect of $y$ is completely replaced by statistical quantities related to the motion of $y$ for a fixed value of $x$. On a more technical note, the precise expression for the quantities entering in the reduced dynamics can be easily obtained through an expansion in $\varepsilon$ of the backward Kolmogorov equation (the adjoint of the Fokker-Planck equation) $\partial_t v (x, t) = (\mathcal{L}_0 +\mathcal{L}_1 / \varepsilon +\mathcal{L}_2 / \varepsilon^2) v (x, t)$ of corresponding to the slow-fast dynamics (where $\mathcal{L}_0 = f_0 \partial_x$, $\mathcal{L}_1 = f_1 \partial_x$ and $\mathcal{L}_2 = g \partial_y$).
The method of homogenisation has found a great number of applications in different fields of physics and mathematics (Pavliotis & Stuart, 2008). Many physical systems, however, do not feature a time scale separation. A relevant example of such a process is convective motion. Convective clouds are significant for the evolution of our climate, yet they can only be resolved at a spatial resolution of 10–100 m (Sakradzija et al., 2015), whereas climate models only resolve scales of the order of 100 km (Intergovernmental Panel on Climate Change, 2013). The unresolved convective motion evolves on range of time scales that overlaps with those of the large scale flow (Sakradzija et al., 2015), therefore homogenisation can not be applied. It is a formidable challenge to derive dimension reduction methods that do not require a time scale separation.
Going beyond the familiar setting of infinite time scale separaration requires a novel approach to the derivation of closed equation for the reduced system.
I have developed a new Edgeworth expansion for slow-fast systems. With this expansion reduced models can be constructed that are accurate over a larger range of the time scale separation parameter $\varepsilon$.
The Edgeworth expansion characterizes the non-Gaussian corrections to the distribution of random variables that converge to a Gaussian distribution, for example due to a central limit theorem (missing reference). In the slow-fast system we have that $(x (\varepsilon) - x (0)) / \varepsilon$ converges to a Gaussian as $\varepsilon \rightarrow 0$, since $x$ converges to an SDE with Gaussian white noise. For finite $\varepsilon$, however, there is a non-zero skewness. In general, the Edgeworth expansions take the form \(\begin{eqnarray*} \rho_{\varepsilon} (x) & = & \mathcal{\mathcal{N}}_{0, \sigma^2} (x) + \varepsilon \kappa H_3 (x) \mathcal{N}_{0, \sigma^2} (x) + o (\varepsilon^2) \end{eqnarray*}\) where $\mathcal{N}_{0, \sigma^2}$ is a Gaussian distribution with zero mean and variance $\sigma^2$, $H_3$ is the third Hermite polynomial and $\varepsilon$ is the small parameter controlling the convergence ($1 / \sqrt{n}$ in the classical central limit theorem or the time scale separation parameter $\varepsilon$. The second term represents the skewness of the distribution, which vanishes as $\varepsilon \rightarrow 0$. I have shown that the variable $(x (\varepsilon) - x (0)) / \varepsilon$ satisfies an Edgeworth expansion and have derived expression for the expansion coefficients (Wouters & Gottwald, 2017).
I have then used this Edgeworth expansion to construct a surrogate system for $y$ that generates the same variance $\sigma^2$ and skewness $\kappa$ for finite values of $\varepsilon$. See Figure 1 for a benchmark of the method on a continuous time slow-fast system where the fast variable is a chaotic Lorenz ‘63 system and the slow variable is a particle in a asymmetric double well potential.
For more details, see (Wouters & Gottwald, 2017)
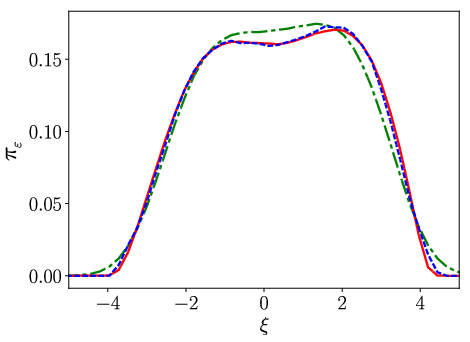
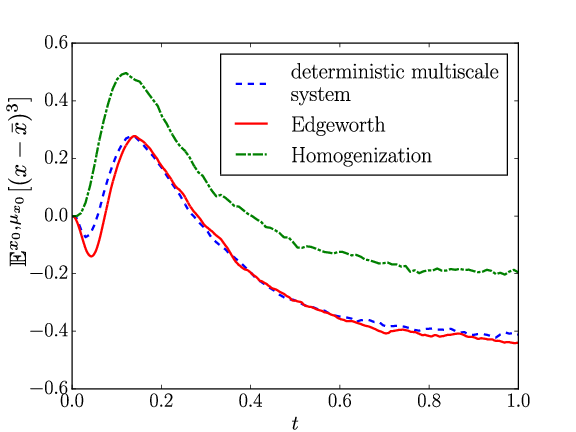
Figure 1: Top: the pdf of the slow variable $x$ in a slow-fast system with a fast chaotic Lorenz ‘63 system acting as noise on a particle in an asymmetric potential well. The pdf of the the standard homogenization method (green) and my Edgeworth expansion based approximation (red) is compared to the truth (blue). Note the much closer approximation of both the bimodal character of the pdf and of the tails by my method. Bottom: the evolution over time of the third moment of the slow variable, as approximated by the homogenised model (green) and by my method (red), the latter again being clearly much closer to the truth (blue). From (Wouters & Gottwald, 2017).
I have furthermore developed a model reduction technique for systems that are weakly coupled (Lucarini et al., 2014; Wouters & Lucarini, 2012; Wouters & Lucarini, 2013). My alternative method for model reduction makes use of a weak coupling approach, in which response theory is used to derive a closure. The systems of interest follow a dynamics determined by
\[\begin{aligned} \dot{x} & = \varepsilon f_1 (x, y) {}+ f_2 (x)\\ \dot{y} & = \varepsilon g_1 (x, y) + g_2 (y),\end{aligned}\]where $x$ is the variable of interest. Exploiting the weak coupling form of this equation, I have employed response theory to expand expectation values of $x$-dependent observable in orders of $\varepsilon$. This expansion yields a series in terms of $\varepsilon$, reminiscent of the Dyson series in scattering theory, each representing a sequence of interactions between the $x$ and $y$ subsystems, corresponding to a certain Feynman diagram.
The truncation of this series up to a given order yields an approximation of the response of the $x$ subsystem to the coupling to the $y$ subsystem. More importantly, it allows to fix the statistical quantities of the $y$ system that determine this repsonse. To first order, for example, this response is simply given by the expectation value $\int d y f_1 (x, y) \rho_2 (y)$, where $\rho_2$ is the invariant density of the uncoupled $\dot{y} = g_2 (y)$ dynamics. To second order a correlation and response function of this uncoupled dynamics appears.
I have exploited this fact to derive a surrogate dynamics for $x$ that reproduces the effect of the coupling of $x$ to $y$ up to second order in $\varepsilon$. By introducing a simplified $y$ dynamics that reproduces the statistical quantities encountered in the response series the statistics of the fully coupled $x$ subsystem can be approximated. The full calculation is detailed in my publications (Wouters & Lucarini, 2012; Wouters & Lucarini, 2013).
I have recently numerically benchmarked this method on a class of low-dimensional slow-fast stochastic systems, previously used as a benchmark by Majda et al. (Majda et al., 2002). My method clearly improves upon the classical homogenisation method. In particular, my weak coupling method gives a marked improved performance over homogenisation in initial ensemble spread (see Fig. 2) and in capturing the statistics of large fluctuations around the mean state, as expressed by expected exit times from a domain (see Table 1). A publication describing these benchmarks is about to be submitted.
My approach does not assume a timescale separation and may therefore be more readily applicable to some problems in geophysical fluid dynamics, such as the parametrisation of atmospheric convection. I am currently co-supervising a PhD student, together with Valerio Lucarini (University of Hamburg & University of Reading) to develop applications in a complex climate model.
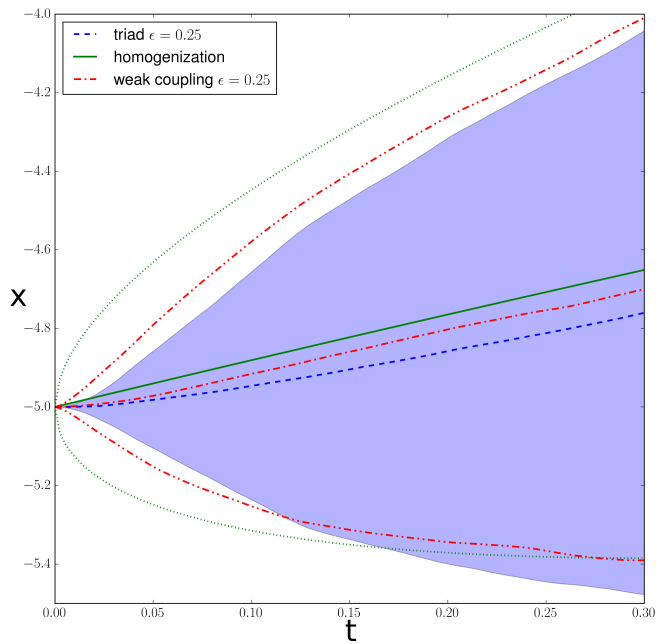
Figure 2: comparison of the ensemble spread for the original triad system for ε=0.25 from an inital condition (-5,0,0) (the ensemble mean is the blue dashed line, 2σ interval the blue shaded area), the two-level Ornstein-Uhlenbeck process from the weak coupling method (7) from an initial condition (-5,0) (ensemble mean: red dash-dotted line, 2σ interval: red dash-dot-dotted lines) and the one-level Ornstein-Uhlenbeck process from homogenization (2) from x=-5 (ensemble mean: green solid line, 2σ interval: dotted lines)
| $\varepsilon$ | 0.5 | 0.25 | 0.125 |
|---|---|---|---|
| homogenisation | 0.403 |
0.184 |
0.0982 |
| weak coupling | 0.205 |
0.0839 |
0.0589 |
Table 1: The relative error on the mean first exit time $e = | \mathbb{E}_1 (\tau) -\mathbb{E}_0 (\tau) | /\mathbb{E}_0 (\tau)$ where $\mathbb{E}_0 (\tau)$ is the mean first exit time from $[- 1, 1]$ of the full triad system (see @majda_priori_2002) and $\mathbb{E}_1 (\tau)$ is the mean exit time of the reduced model (either obtained through homogenisation or my weak coupling method). The errors are almost halved with the weak coupling method.
- Huisinga, W., Schütte, C., & Stuart, A. M. (2003). Extracting macroscopic stochastic dynamics: Model problems. Communications on Pure and Applied Mathematics, 56(2), 234–269. https://doi.org/10.1002/cpa.10057
- Givon, D., Kupferman, R., & Stuart, A. (2004). Extracting macroscopic dynamics: model problems and algorithms. Nonlinearity, 17(6), R55–R127. https://doi.org/10.1088/0951-7715/17/6/R01
- Hijón, C., Español, P., Vanden-Eijnden, E., & Delgado-Buscalioni, R. (2009). Mori-Zwanzig formalism as a practical computational tool. Faraday Discussions, 144, 301–322.
- Lu, J., & Vanden-Eijnden, E. (2014). Exact dynamical coarse-graining without time-scale separation. The Journal of Chemical Physics, 141(4), 044109. https://doi.org/10.1063/1.4890367
- Lucarini, V., Blender, R., Herbert, C., Ragone, F., Pascale, S., & Wouters, J. (2014). Mathematical and physical ideas for climate science. Reviews of Geophysics, 52(4), 809–859. https://doi.org/10.1002/2013RG000446
- Imkeller, P., & von Storch, J.-S. (2001). Stochastic climate models. Birkhäuser.
- Palmer, T. N., & Williams, P. (2009). Stochastic Physics and Climate Modelling. Cambridge University Press.
- Pavliotis, G. A., & Stuart, A. M. (2008). Multiscale methods. Springer.
- Sakradzija, M., Seifert, A., & Heus, T. (2015). Fluctuations in a quasi-stationary shallow cumulus cloud ensemble. Nonlin. Processes Geophys., 22(1), 65–85. https://doi.org/10.5194/npg-22-65-2015
- Intergovernmental Panel on Climate Change. (2013). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press.
- Wouters, J., & Gottwald, G. A. (2017). Edgeworth expansions for slow-fast systems and their application to model reduction for finite time scale separation. ArXiv:1708.06984 [Nlin]. http://arxiv.org/abs/1708.06984
- Wouters, J., & Lucarini, V. (2012). Disentangling multi-level systems: averaging, correlations and memory. Journal of Statistical Mechanics: Theory and Experiment, 2012(03), P03003. https://doi.org/10.1088/1742-5468/2012/03/P03003
- Wouters, J., & Lucarini, V. (2013). Multi-level Dynamical Systems: Connecting the Ruelle Response Theory and the Mori-Zwanzig Approach. Journal of Statistical Physics, 151(5), 850–860. https://doi.org/10.1007/s10955-013-0726-8
- Majda, A., Timofeyev, I., & Vanden-Eijnden, E. (2002). A priori tests of a stochastic mode reduction strategy. Physica D: Nonlinear Phenomena, 170(3–4), 206–252. https://doi.org/10.1016/S0167-2789(02)00578-X